统计glm_统计GLM

统计glm_统计GLM _统计GLM

       最近有些忙碌，今天终于有时间和大家聊一聊“统计glm”的话题。如果你对这个话题还比较陌生，那么这篇文章就是为你而写的，让我们一起来探索其中的奥秘吧。

1.比较线性回归模型和广义线性模型两类方法的异同

2.spss医学统计的问题，急求解~应该用什么方法啊~

3.方差分析与回归分析的异同

4.数据分析

比较线性回归模型和广义线性模型两类方法的异同

       logistic回归：

       Logistic回归的应用条件是：

       ① 独立性。各观测对象间是相互独立的；

       ② LogitP与自变量是线性关系；

       ③ 样本量。经验值是病例对照各50例以上或为自变量的5-10倍（以10倍为宜），不过随着统计技术和软件的发展，样本量较小或不能进行似然估计的情况下可采用精确logistic回归分析，此时要求分析变量不能太多，且变量分类不能太多；

       ④ 当队列资料进行logistic回归分析时，观察时间应该相同，否则需考虑观察时间的影响（建议用Poisson回归）。

       logistic回归一般是用来解决二元分类问题，它是从贝努力分布转换而来的

       hθ(x) = g(z)=1/1+e-z ;z=θTx

       最大似然估计L(θ) = p(Y|X;θ)

        =∏p(y(i)|x(i);θ)

        =∏(hθ(x))y(i)(1-hθ(x))1-y(i)

        ?l(θ) = logL(θ)

        =Σy(i)loghθ(x(i))+(1-y(i))log(1-hθ(x(i)))

       　 ?θ的优化目的就是让最大似然估计最大，用梯度上升法求θ

       θj=θj+α?l(θ)/?θj=θj+α(y(i)-hθ(x(i)))x(i)j

       logistic回归用梯度上升法求得的θ的迭代公式看起来跟线性回归很像，但这跟线性回归是有本质区别的

       1.线性回归是由高斯分布推导而来，而logistic回归是由贝努力分布推导而来

       2.二种回归的最大似然估计是不一样的，只不过求完导后的结果看似相同

        ? 3.二种回归hθ(x)是不同的

       广义线性模型：

       广义线性模型是线性模型的扩展，其特点是不强行改变数据的自然度量，数据可以具有非线性和非恒定方差结构[59]，主要是通过联结函数g()(link function)，建立响应变量Y的数学期望值 与线性组合的预测变量P之间的关系：。与线性模型相比，GLM模型中Y的分布可以是任何形式的指数分布（如高斯分布、泊松分布、二项式分布），联结函数可以是任何单调可微函数（如对数函数logarithm 或逻辑函数logit）。Y的方差通过方程函数 依赖于其数学期望值 ，这里 ，为比例（或者称为离差）参数[57-58,60]。这些优点使得GLM模型可以处理非正态分布的响应变量，同时可包含定性、半定量的预测变量；Y通过连接函数g(E(Y))与线性预测因子P建立联系，不仅确保线性关系，且可保证预测值落在响应变量的变幅内，并可解决数据过度离散的问题，从而使GLM逐渐成为植被-环境关系研究的重要模型，并得到越来越多的关注。

       之前已经写了线性回归和logistic回归，基本的形式都是先设定hθ(x)，然后求最最大似然估计L(θ),然后求出l(θ)=logL(θ),然后用梯度上升法或其它方法求出θ，二种回归如此想你的原因就是在于它都都是广义线性模型里的一员。

       如果一个概念分布可以表示成p(y;η)=b(y)exp(ηTT(y)-a(η))时，那么这个概率分布可以称之为指数分布

       贝努力分布转换为指数分布：p(y;?)=?y(1-?)1-y

       　　　　　　　　 =exp(log(?y(1-?)1-y))

       　　　　　　　　 =exp(ylog?+(1-y)log(1-?))

       　　　　　　　　 =exp((log(?/(1-?)))y+log(1-?))

       根据上面指数分布的公式可得出：

       　　　　　 ?b(y)=1

       　　　　　 ?η=log?/(1-?);?=1/(1+e-η)

       　　　　　 ?T(y) = y

       　　　　　 ?a(η)=-log(1-?)

       高斯分布转换为指数(因为σ的取值对最后的结果没影响，所以设σ2=1)：p(y;μ)=(1/2π)exp(-1/2(y-μ)2);2π上有根号

        ? =(1/2π)exp(-1/2y2).exp(μy-1/2μ2)

       根据上面指数分布的公式可得出：

       　　　　　 b(y)=(1/2π)exp(-1/2y2);2π上有根号

        η=μ

        T(y) = y

        a(η)=1/2μ2

       广义线性模型的三步是：

       1.将y|x;θ变换成以η为参数的指数分布的形式

       　 ? 2.因为h(x)=E[y|x],所以能过第1步的变换可以得到E[y|x]与η的对应关系(对于logistic回归，期望值是?，?与η的关系是?=1/(1+e-η)；对于线性回归，期望值是μ，μ与η的关系是η=μ)

       3.设定η=θTx(如果η是一个向量值的话，那么ηi=θiTx)

spss医学统计的问题，急求解~应该用什么方法啊~

        原先三个样本的HTSeq-count计数的数据可以在我的GitHub中找到，但是前面已经说过Jimmy失误让我们分析的人类就只有3个样本， 另外一个样本需要从另一批数据获取（请注意batch effect)，所以不能保证每一组都有两个重复。

        我一直坚信”你并不孤独“这几个字，遇到这种情况的人肯定不止我一个，于是我找到了几种解决方法

        以上方法都会在后续进行介绍，但是我们DESeq2必须得要有重复的问题亟待解决，没办法我只能自己瞎编了。虽然是编，我们也要有模有样，不能直接复制一份，要考虑到高通量测序的read是默认符合泊松分布的。我是这样编的。

        这仅仅是一种填坑的方法而已，更好模拟数据的方法需要参阅更加专业的文献， 有生之年 我希望能补上这一个部分。

        这部分内容最先在 RNA-Seq Data Analysis 的8.5.3节看到，刚开始一点都不理解，但是学完生物统计之后，我认为这是理解所有差异基因表达分析R包的关键。

        基本上，统计课都会介绍如何使用t检验 用来比较两个样本之间的差异，然后在样本比较多的时候使用方差分析 确定样本间是否有差异。当然前是样本来自于正态分布的群体，或者随机独立大量抽样。

        对于基因芯片的差异表达分析而言，由于普遍认为其数据是服从正态分布，因此差异表达分析无非就是用t检验和或者方差分析应用到每一个基因上。高通量一次性找的基因多，于是就需要对多重试验进行矫正，控制假阳性。目前在基因芯片的分析用的最多的就是limma 。

        但是 ，高通量测序(HTS)的read count普遍认为是服从泊松分布（当然有其他不同意见），不可能直接用正态分布的t检验 和方差分析 。 当然我们可以简单粗暴的使用对于的非参数检验 的方法，但是统计力不够，结果的p值矫正之估计一个差异基因都找不到。老板花了一大笔钱，结果却说没有差异基因，是个负结果，于是好几千经费打了水漂，他肯定是不乐意的。因此，还是得要用参数检验的方法，于是就要说到方差分析和线性模型之间的关系了。

        线性回归和方差分析是同一时期发展出的两套方法。在我本科阶段的田间统计学课程中就介绍用方差分析 （ANOVA）分析不同肥料处理后的产量差异，实验设计如下

        这是最简单的单因素方差分析，每一个结果都可以看成 yij = ai + u + eij， 其中u是总体均值，ai是每一个处理的差异，eij是随机误差。

        注 ：方差分析(Analysis of Variance, ANAOVA)名字听起来好像是检验方差，但其实是为了判断样本之间的差异是否真实存在，为此需要证明不同处理内的方差显著性大于不同处理间的方差。

        线性回归 一般是用于量化的预测变量来预测量化的响应变量。比如说体重与身高的关系建模：

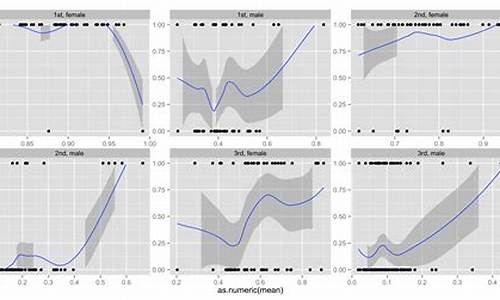
        当然线性回归也可用处理名义型或有序型因子（也就是离散变量）作为预测变量，如果要画图的话，就是下面这个情况。

        如果我们需要通过一个实验找到不同处理后对照组和控制组的基因变化，那么基因表达可以简单写成， y = a + b · treament + e。 和之前的 yij = ai + u + eij 相比，你会发现公式是如此的一致。 这是因为线性模型和方差分析都是广义线性模型 (generalizing linear models, GLM)在正态分布的预测变量的特殊形式。而GLM本身只要采用合适的连接函数 是可以处理对任意类型的变量进行建模的。

        目前认为read count之间的差异是符合负二项分布，也叫gamma-Possion分布。那么问题来了，如何用GLM或者LM分析两个处理件的差异呢？其实可以简单的用上图的拟合直线的斜率来解释，如果不同处理之间存在差异，那么这个拟合线的斜率必定不为零，也就是与X轴平行。但是这是一种便于理解的方式（虽然你也未必能理解），实际更加复杂，考虑因素更多。

        注1 负二向分布有两个参数，均值(mean)和离散值（dispersion). 离散值描述方差偏离均值的程度。泊松分布可以认为是负二向分布的离散值为1，也就是均值等于方差（mean=variance）的情况。

注2 这部分涉及大量的统计学知识，不懂就用维基百科一个个查清楚。

        聊完了线性模型和方差分析，下面的设计矩阵（design matrix）就很好理解了， 其实就是用来告诉不同的差异分析函数应该如何对待变量。比如说我们要研究的KD和control之间变化，设计矩阵就是

        那么比较矩阵（contrast matrix)就是告诉差异分析函数应该如何对哪个因素进行比较， 这里就是比较不同处理下表达量的变化。

        其实read count如何标准化的方法有很多，最常用的是FPKM和RPKM，虽然它们其实是错的-- FPKM/RPKM是错的 。

        我推荐阅读 Comparing the normalization methods for the differential analysis of Illumina high-throughput RNA-Seq data , 了解不同标准化方法之间的差异。

        有一些方法是要求原始数据，有一些则要求经过某类标准化后的数据，记得区分。

        关于DESeq2分析差异表达基因，其实在 position bias)标准化。edgeR的 calcNormFactors 函数使用TMM算法 对DGEList标准化

        注 大部分的mRNA-Seq数据分析用TMM标准化就行了，但是也有例外，比如说single-cell RNA-Seq(Lun, Bach, and Marioni 2016), 还有就是global differential expression， 基因组一半以上的基因都是差异表达的，请尽力避免，(D. Wu et al. 2013)， 不然就需要用到内参进行标准化了(Risso et al. 2014).

        第四步： 实验设计矩阵(Design matrix)， 类似于DESeq2中的design参数。 edgeR的线性模型和差异表达分析需要定义一个实验设计矩阵。很直白的就能发现是1vs0

        第五步： 估计离散值（Dispersion）。前面已经提到负二项分布（negative binomial，NB)需要均值和离散值两个参数。edgeR对每个基因都估测一个经验贝叶斯稳健离散值（mpirical Bayes moderated dispersion），还有一个公共离散值（common dispersion，所有基因的经验贝叶斯稳健离散值的均值）以及一个趋势离散值

        还可以进一步通过quasi-likelihood (QL)拟合NB模型，用于解释生物学和技术性导致的基因特异性变异 (Lund et al. 2012; Lun, Chen, and Smyth 2016).

        注1 估计离散值这个步骤其实有许多 estimate*Disp 函数。当不存在实验设计矩阵(design matrix)的时候， estimateDisp 等价于 estimateCommonDisp 和 estimateTagwiseDisp 。而当给定实验设计矩阵(design matrix)时， estimateDisp 等价于 estimateGLMCommonDisp , estimateGLMTrendedDisp 和 estimateGLMTagwiseDisp 。 其中tag与gene同义。

        注2 其实这里的第三， 四， 五步对应的就是DESeq2的 DESeq 包含的2步，标准化和离散值估测。

        第六步: 差异表达检验（1）。这一步主要构建比较矩阵，类似于DESeq2中的 results 函数的 contrast 参数。

        这里用的是 glmQLFTest 而不是 glmLRT 是因为前面用了glmQLTFit进行拟合，所以需要用QL F-test进行检验。如果前面用的是 glmFit ，那么对应的就是 glmLRT . 作者称QL F-test更加严格。多重试验矫正用的也是BH方法。

        后续就是提取显著性差异的基因用作下游分析，做一些图看看

        第六步：差异表达检验（2）。上面找到的显著性差异的基因，没有考虑效应值，也就是具体变化了多少倍。我们也可用找表达量变化比较大的基因，对应的函数是 glmTreat 。

        经过上面两个方法的洗礼，基本上套路你也就知道了，我先简单小结一下，然后继续介绍limma包的 voom 。

        Limma原先用于处理基因表达芯片数据，可是说是这个领域的老大 :sunglasses: 。如果你仔细看edgeR导入界面，你就会发现，edgeR有一部分功能依赖于limma包。Limma采用经验贝叶斯模型（ Empirical Bayesian model）让结果更稳健。

        在处理RNA-Seq数据时，raw read count先被转成log2-counts-per-million (logCPM)，然后对mean-variance关系建模。建模有两种方法：

        数据预处理 ： Limma使用edgeR的DGEList对象，并且过滤方法都是一致的，对应edgeR的第一步,第二步， 第三步

        差异表达分析 : 使用”limma-trend“

        差异表达分析 : 使用”limma-voom“

        如果分析基因芯片数据，必须好好读懂LIMMA包。

        基本上每一个包，我都提取了各种的显著性基因，比较就需要用韦恩图了，但是我偏不 :stuck_out_tongue: 我要用UpSetR.

        感觉limma的结果有点奇怪，有生之年在折腾吧。

        好吧，这部分我鸽了

        [1] Comparing the normalization methods for the differential analysis of Illumina high-throughput RNA-Seq data

        [2] https://www.bioconductor.org/help/workflows/rnaseqGene/

        [3] https://www.bioconductor.org/help/workflows/RnaSeqGeneEdgeRQL/

        [4] https://www.bioconductor.org/help/workflows/RNAseq123/

方差分析与回归分析的异同

       分别做男性不同年龄段和女性不同年龄段的方差分析：1. 先将男女分开，分别放在不同的SPSS表格中。2. 将不同的年龄段进行排序，例如：<20设为1，20-30设定为2，依次类推。 3. 在SPSS中选择Analyze→Compare Means→One-Way ANOVA，打开对话框以后，将血红蛋白含量添加到Dependent List中，将第二步中的排序变量放在Factor中。 4. 均值和均差：在Options选项中将Descriptive和Homogeneity variance test选中，→Continue。 5. 两两比较：在Post Hoc选项中将LSD或S-N-K或其他两两比较法选中，看你需要用的是什么方法了，→Continue。 6. 点击OK，就会出来你想要的结果了！（完全自撰）

数据分析

       一、方差分析与回归分析的相同点

       1、方差分析与回归分析的变量都是两种或两种以上。

       2、方差分析与回归分析的结果都是得出因变量和自变量之间的关系。

       二、方差分析与回归分析的不同点

       1、原理不同

       方差分析：方差分析的基本原理是认为不同处理组的均数间的差别基本来源有两个，分别为实验条件和?随机误差。

       回归分析：回归分析的原理是利用实验获得的数据构建解释变量对响应变量的线性模型，当利用这个解释模型来预测未知数据时为预测模型。

       2、分析方法不同

       方差分析：方差分析的分析方法主要是单因素方差分析、两因素方差分析。

       回归分析：回归分析的分析方法主要是线性回归分析、非线性回归分析。

       3、应用不同

       方差分析：方差分析主要应用于均数差别的显著性检验、分离各有关因素并估计其对总变异的作用、分析因素间的交互作用和方差齐性检验。

       回归分析：回归分析主要应用于预测分析、时间序列模型以及发现变量之间的因果关系。

       百度百科-回归分析

        百度百科-方差分析

       1、按照计量精确程度，由高到低可分为定比尺、定距尺度、定序尺度、定类尺度。

        a.定类尺度：也称类别尺度或名义尺度，是将调查对象分类，标以各种名称，并确定其类别的方法。它实质上是一种分类体系。

        b.定序尺度：也称等级尺度或顺序尺度，是按照某种逻辑顺序将调查对象排列出高低或大小，确定其等级及次序的一种尺度。

        c.定距尺度：也称等距尺度或区间尺度，是一种不仅能将变量（社会现象）区分类别和等级，而且可以确定变量之间的数量差别和间隔距离的方法。

        d.定比尺度：也称比例尺度或等比尺度，是一种除有上述三种尺度的全部性质之外，还有测量不同变量（社会现象）之间的比例或比率关系的方法。

        2、受极端数值影响较小的集中趋势值是众数和中位数。

        3、用决策树进行分析时，采用的方式是反推。

        4、推断统计学研究如何根据样本数据去推断总体数量特征的方法。

        描述统计学(descriptive statistics)是研究如何取得反映客观现象的数据(data tabulation)，并通过图表形式对所搜集的数据进行加工处理和显示(data visualisation)，进而通过综合概括与分析(statistical summaries)得出反映客观现象的规律性数量特征的一门学科。

        5、描述统计与推断统计有何区别和联系？

        区别：描述统计研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。推断统计是研究如何利用样本数据来推断总体特征的方法。

        联系：描述统计学和推断统计学是现代统计学的两个组成部分呢，相辅相成、缺一不可，描述统计学是现代统计学的基础和前提，推断统计学是现代统计学的核心和关键。

        6、R中，使用哪一个函数进行logit回归？

        glm

        7、bootstrap

        Bootstrap方法根据给定的原始样本复制观测信息对总体的分布特性进行统计推断，不需要额外的信息，Efron（1979）认为该方法也属于非参数统计方法。Bootstrap方法从观察数据出发，不需任何分布假定，针对统计学中的参数估计及假设检验问题，利用Bootstrap方法产生的自举样本计算的某统计量的数据集可以用来反映该统计量的抽样分布，即产生经验分布，这样，即使我们对总体分布不确定，也可以近似估计出该统计量及其置信区间，由此分布可得到不同置信水平相应的分位数——即为通常所谓的临界值，可进一步用于假设测验。因而，Bootstrap方法能够解决许多传统统计分析方法不能解决的问题。在Bootstrap的实现过程中，计算机的地位不容忽视(Diaconis et al.,1983)，因为Bootstrap涉及到大量的模拟计算。可以说如果没有计算机，Bootstrap理论只可能是一纸空谈。随着计算机的快速发展，计算速度的提高，计算费时大大降低。在数据的分布假设太牵强或者解析式太难推导时，Bootstrap为我们提供了解决问题的另一种有效的思路。因此，该方法在生物科学研究中有一定的利用价值和实际意义

       　非参数统计中一种重要的估计统计量方差进而进行区间估计的统计方法,也称为自助法.其核心思想和基本步骤如下：

        （1） 采用重采样技术从原始样本中抽取一定数量（自己给定）的样本,此过程允许重复抽样.

        （2） 根据抽出的样本计算给定的统计量T.

        （3） 重复上述N次（一般大于1000）,得到N个统计量T.

        （4） 计算上述N个统计量T的样本方差,得到统计量的方差.

        应该说Bootstrap是现代统计学较为流行的一种统计方法,在小样本时效果很好.通过方差的估计可以构造置信区间等,其运用范围得到进一步延伸.

        具体抽样方法举例：想要知道池塘里面鱼的数量,可以先抽取N条鱼,做上记号,放回池塘.

        进行重复抽样,抽取M次,每次抽取N条,考察每次抽到的鱼当中有记号的比例,综合M次的比例,在进行统计量的计算.。

        8、统计对现象总体数量特征的认识是从个体到总体。

        9、抽样误差与非抽样误差有什么区别？

        抽样误差：抽样方法本身所引起的误差。当由总体中随机地抽取样本时，哪个样本被抽到是随机的，由所抽到的样本得到的样本指标x与总体指标μ之间偏差，称为实际抽样误差。举个列子，为了方便计算我就举小的列子，自己可以放大，10个男生 身高有3个为170,4个为175,3个为180, 平均身高为175，抽样抽了5个人，分别是170，175,175,175,175，很明显就存在误差了。

        非抽样误差是指除抽样误差以外所有的误差的总和。引起非抽样误差的原因很多，比如抽样框不齐全，访问员工作经验有限，被访者不配合访问而加以虚假的回答，问卷设计本身存在缺陷等等。

        10、研究者想收集证据予以支持的假设通常称原假设。

        11、根据统计分析方法的研究和应用来分，可将统计学分为理论统计学和应用统计学。

        12、统计分组的关键在于选择分组标志和划分相邻两组间的界限。

        13、下面的哪一个误差属于随机误差？（A）

        A．随机误差 B．抽样框误差C．回答误差D．无回答误差

        14、小钱收集了上海、江苏和浙江三省2007年三次产业的增加值的资料，如果要反映2007年这三个省三次产业的结构，用什么图形最为合适？（）

        A.直方图 B.散点图 C.饼图 D.折线图

        15、tableau文件类型： .twb .tds .tde .bat

        16、以一、二、三等品来衡量产品质地的优劣，那么该产品等级是（D）。

        A.品质标志 B.数量标志 C.质量指标 D.数量指标

       今天关于“统计glm”的探讨就到这里了。希望大家能够更深入地了解“统计glm”，并从我的答案中找到一些灵感。