三角形欧拉定理_三角形欧拉定理证明

三角形欧拉定理_三角形欧拉定理证明 _三角形欧拉定理证明

       最近有些日子没和大家见面了，今天我想和大家聊一聊“三角形欧拉定理”的话题。如果你对这个领域还比较陌生，那么这篇文章就是为你而写的，让我们一起来探索其中的奥秘吧。

1.欧拉公式三种形式

2.在几何学中欧拉三角形有何重要性？

3.欧拉定理 欧拉方程的原理是什么 它到底要说明一个什么？

欧拉公式三种形式

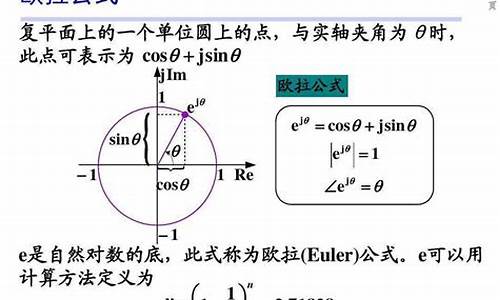
       欧拉公式三种形式分别是：分式里的欧拉公式=a＾r/(a-b)(a-c)+b＾r/(b-c)(b-a)+c＾r/(c-a)(c-b)，复变函数论里的欧拉公式为e^ix=cosx+isinx，三角形中的欧拉公式为d＾2=R＾2-2Rr。

       一、把复指数函数与三角函数联系起来的一个公式，e是自然对数的底，i是虚数单位。它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它不仅出现在数学分析里，而且在复变函数论里也占有非常重要的地位，更被誉为“数学中的天桥”。

       二、复变函数论中的欧拉公式证明：

       1、当R=2时，由说明这两个区域可想象为以赤道为边界的两个半球面，赤道上有两个“顶点”将赤道分成两条“边界”，即R=2，V=2，E=2，于是R+V-E=2，欧拉定理成立。

       2、设R=m(m≥2)时欧拉定理成立，下面证明R=m+1时欧拉定理也成立。由说明我们在R=m+1的地图上任选一个区域X，则X必有与它如此相邻的区域Y，使得在去掉X和Y之间的唯一一条边界后，地图上只有m个区域了。

       3、在去掉X和Y之间的边界后，若原该边界两端的顶点现在都还是3条或3条以上边界的顶点，则该顶点保留，同时其他的边界数不变；若原该边界一端或两端的顶点现在成为2条边界的顶点，则去掉该顶点，该顶点两边的两条边界便成为一条边界。

在几何学中欧拉三角形有何重要性？

       三角形的外心、重心、九点圆圆心、垂心，依次位于同一直线上，这条直线就叫三角形的欧拉线。

       欧拉于1765年在它的著作《三角形的几何学》中首次提出定理：三角形的重心在欧拉线上，即三角形的重心、垂心和外心共线。

       欧拉线的证明：

       作△ABC的外接圆，连结并延长BO，交外接圆于点D。连结AD、CD、AH、CH、OH。作中线AM，设AM交OH于点G’。 ∵ BD是直径， ∴ ∠BAD、∠BCD是直角。 ∴ AD⊥AB，DC⊥BC。 ∵ CH⊥AB，AH⊥BC， ∴ DA‖CH，DC‖AH。 ∴ 四边形ADCH是平行四边形， ∴ AH=DC。 ∵ M是BC的中点，O是BD的中点。 ∴ OM= DC。 ∴ OM= AH。 ∵ OM‖AH， ∴ △OMG’ ∽△HAG’。 ∴ 。 ∴ G’是△ABC的重心。 ∴ G与G’重合。 ∴ O、G、H三点在同一条直线上。

       在平面几何中，欧拉线（图中的红线）是指过三角形的垂心（蓝）、外心（绿）、重心（黄）和九点圆圆心（红点）的一条直线。莱昂哈德·欧拉证明了在任意三角形中，以上四点共线。欧拉线上的四点中，九点圆圆心到垂心和外心的距离相等，而且重心到外心的距离是重心到垂心距离的一半。

       [编辑]证明

       如图，H、G、O分别是△ABC的垂心、重心、外心，连AH，作△ABC的外接圆直径BOD，再连DB、DA，则DC⊥BC…①，DA⊥AB…②

       ∵H为△ABC垂心 ∴AH⊥BC…③，CH⊥AB…④

       由①、③可知DC‖AH，由②、④可知DA‖CH，故四边形ADCH为平行四边形，∴AH=DC。∵点O与点M分别是BD、CB的中点 ∴DC=2OM，即AH=2OM。作BC边上的中线AM,连OM、OH；设OH交AM与点G’

       ∵OM⊥BC，△AHG’∽△MOG’，∴AG’=2G’M，因此G’即△ABC重心G。

       故△ABC的垂心H、重心G和外心O三点共线，直线HGO即欧拉线。

       [

欧拉定理 欧拉方程的原理是什么 它到底要说明一个什么？

       欧拉三角形是几何学中的一个重要概念，它由三个顶点和三条边组成。这个三角形的重要性体现在以下几个方面：

       1.欧拉定理：欧拉三角形与欧拉定理密切相关。欧拉定理是关于多边形的顶点数（V）、边数（E）和面数（F）之间关系的定理。在欧拉三角形中，有V=E+2=F+1的关系。这个定理对于解决多边形的问题非常有用，例如计算一个多面体的边数或面数。

       2.拓扑学：欧拉三角形在拓扑学中也扮演着重要的角色。拓扑学研究的是空间的性质和结构，而欧拉三角形可以用来描述拓扑空间的一些特征。例如，欧拉公式可以用来计算一个拓扑空间的欧拉特征数，该特征数反映了空间的连通性和孔洞的数量。

       3.图论：欧拉三角形与图论也有密切的关系。图论是研究图形和网络结构的数学分支，而欧拉三角形可以用来构建一些特殊的图。例如，欧拉回路是一个通过图中每个边恰好一次且回到起点的路径，而欧拉通路是一个通过图中每个边恰好一次但不回到起点的路径。这些概念在图论中有广泛的应用，例如在电路设计、网络优化等领域。

       4.美学：欧拉三角形在美学上也有一定的意义。它的构造和性质给人一种对称和平衡的感觉，因此在艺术和设计中经常被使用。例如，欧拉三角形可以用于设计建筑物的立面、装饰品的形状等。

       综上所述，欧拉三角形在几何学中具有重要的地位。它不仅与欧拉定理、拓扑学和图论等数学领域密切相关，还在美学上有一定的应用价值。因此，对欧拉三角形的研究和应用有助于我们更好地理解和探索几何学和其他相关学科的奥秘。

       1、初等数论中的欧拉定理定理：

        在数论中，欧拉定理（也称费马-欧拉定理）是一个关于同余的性质。

        欧拉定理表明，若n,a为正整数，且n,a互素，(a,n) = 1，则a^φ(n) ≡ 1 (mod n)

       2、平面几何里的欧拉定理定理内容

        设三角形的外接圆半径为R，内切圆半径为r，外心与内心的距离为d，则d^2=R^2-2Rr．

       3、拓扑学里的欧拉公式

        V+F-E=X(P)，V是多面体P的顶点个数，F是多面体P的面数，E是多面体P的棱的条数,X(P)是多面体P的欧拉示性数。

        如果P可以同胚于一个球面（可以通俗地理解为能吹胀成一个球面），那么X(P)=2，如果P同胚于一个接有h个环柄的球面，那么X(P)=2-2h。

        X(P)叫做P的拓扑不变量，是拓扑学研究的范围。

       4、经济学中的“欧拉定理”（这个我看不懂也理解不来，网上查的资料，你参考看看）

        在西方经济学里，产量和生产要素L、K的关系表述为Q＝Q(L，K)，如果具体的函数形式是一次齐次的，那么就有：Q＝L(?Q/?L)＋K(?Q/?K)，换句话说，产品分配净尽取决于Q能否表示为一个一次齐次函数形式。

        因为?Q/?L＝MPL＝w/P被视为劳动对产量的贡献，?Q/?K＝MPK＝r/P被视为资本对产量的贡献，因此，此式被解释为“产品分配净尽定理”，也就是所有产品都被所有的要素恰好分配完而没有剩余。因为形式上符合数学欧拉定理，所以称为欧拉定理。

       5、复变函数论里的欧拉公式定理内容（这个我看不懂也理解不来，网上查的资料，你参考看看）

        e^ix=cosx+isinx e是自然对数的底，i是虚数单位。

        它将三角函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位。

        公式里的x换成-x，得到：e^-ix=cosx-isinx，然后采用两式相加减的方法得到：

        sinx=(e^ix-e^-ix)/(2i)，cosx=(e^ix+e^-ix)/2. 这两个也叫做欧拉公式。

       这些资料希望对你有点点帮助！我也是网上找的...

       好了，关于“三角形欧拉定理”的话题就到这里了。希望大家通过我的介绍对“三角形欧拉定理”有更全面、深入的认识，并且能够在今后的实践中更好地运用所学知识。